(edX stanfordOnline Databases: Modeling and Theory) Relational Algebra 2 (Set operators, renaming, notation)

* Relational algebra query or expression on set of relations produces relation as a result

다음과 같은 테이블이 있다고 하자.

Colleage(cName, state, enrollment)

Student(sID, sName, GPA, sizeHS)

Apply(sID, cName, major, decision)

 

* Union operator

ex. List of college and student names를 구하자.

join은 horizontally combine한다.

이 경우는 vertically combine 해야 한다.

 

union 하려면 schema가 같아야 한다. 컬럼명이 같아야 한다.

 

* Difference operator

ex. IDs of students who didn't apply to any colleges

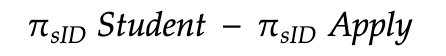
It will take all IDs of the students and then subtract the ones who have applied somewhere.

 

ex. IDs and names of students who didn't apply to any colleges

wrong!

Apply table에는 sName이 없기 때문에 이렇게 할 수는 없다

join back을 해야 한다

IDs를 구한 후 studen relation과 조인해야 한다.

 

* Intersection operator

교집합도 피연산자들의 스키마가 모두 동일해야 연산 가능하다.

 

ex. Names that are both a college name and a student name

Intersection doesn't add expressive power.

그럼 다른 연산자만으로 어떻게 구현할 수 있을까?

* Rename operator

 

Greek Symbol rho를 사용한다.

릴레이션의 이름, 혹은 속성의 이름을 바꾸기 위해 사용한다.

 

(1) 우리가 앞서 살펴보았던 합집합, 차집합, 교집합 연산은 스키마가 같을 때만 사용할 수 있다.

College, Student, Apply 릴레이션의 스키마는 같지 않다.

이런 상황에서 Rename operator를 사용한다.

 

(2) disambiguation in self-join에서도 사용한다.

ex. Pairs of colleges in same state를 구하는 문제

 

college join college making the state equal를 해야 한다.

위 두 가지 방식으로 하면

(Stanford, Berkeley) 뿐만 아니라
(Stanford, Stanford), (Berkeley, Berkeley)도 쿼리된다.

 

해결: 앞에 n1과 n2가 다르다는 selection operator를 추가한다

 

하지만 또 문제점이 있다.

(Stanford, Berkeley), (Berkeley, Stanford)가 같이 쿼리된다.

 

해결: 부등호를 사용한다. first one is less than the second

(Berkeley, Stanford)가 쿼리된다.

 

 

ex. Suppose relation Student has 20 tuples. What is the minimum and maximum number of tuples in the result of this expression:

minimum = 20, maximum = 400

 

minimum: 모든 튜플의 g-h combination이 유니크할 때, join only with themselves

maximum: g-h가 모두 동일할 때

 

* Assignment Statement

 

관계대수에서 어떤 식의 결과를 변수에 할당하는 문장

 

modularize(부분별로 나누어 구조화)하고 싶을 때 사용한다.

 

* Expression tree