(edX stanfordOnline Databases: Modeling and Theory) Multivalued Dependencies and

Apply 릴레이션에 FD가 없다.
FD가 없으면 모든 속성이 키다.
BCNF는 모든 Function Dependencies(X -> Y)에 대해 left hand side(왼쪽, X)이 릴레이션의 슈퍼키다.
이 케이스는 BCNF 맞다.
 
하지만 좋은 디자인은 아니다.
한 학생이 5개의 대학에 지원하고, 6개의 취미가 있다면, 튜플이 30개가 되기 때문.
대학과 취미가 독립적이라면 분해해야 한다.
 
The separation of independent facts is what fourth normal form is about.
 
 

A ↠ B

double headed arrow
"A" multi determines "B"
같은 A 값을 가진 튜플들끼리는, 그들의 B값들이 독립적으로 모든 조합을 이뤄야 한다.
 

같은 A 값을 가진 튜플이 있다면,
그 A에 대응하는 B 값들이 C와 독립적으로 조합될 수 있어야 한다는 뜻

(여기서 C는 R - A - B, 즉 나머지 속성들)
 
ex. 릴레이션 R(Student, Hobby, Language)
 
학생마다 여러 Hobby를 가질 수 있고,
여러 Language도 할 수 있는데,
Hobby와 Language는 서로 관련이 없다고 가정해보자.
즉:

• 학생이 어떤 취미를 가지는지
• 학생이 어떤 언어를 하는지는
  각자 독립된 정보라는 뜻

---

✅ 이때 다치 종속이란?

Student ⟶⟶ Hobby
Student ⟶⟶ Language

이렇게 두 개의 MVD가 있다고 할 수 있다.
의미

같은 Student에 대해,
모든 Hobby 값이 모든 Language 값과 쌍으로 조합된 튜플이 있어야 함

즉, 조합된 결과가 릴레이션 안에 있어야 한다.

---

🔍 표로 보면:

Student Hobby Language

Alice	Swimming	English
Alice	Swimming	Japanese
Alice	Reading	English
Alice	Reading	Japanese

→ 이렇게 4개 조합이 모두 있으면
→ Student ⟶⟶ Hobby, Student ⟶⟶ Language 모두 성립

---

❌ 그런데 조합이 빠지면?

Student	Hobby	Language
Alice	Swimming	English
Alice	Swimming	Japanese
Alice	Reading	English

여기서는 Alice - Reading - Japanese 이 빠졌다.
의미

• Alice는 Swimming, Reading 을 좋아함
• Alice는 English, Japanese 를 한다

그런데 Reading + Japanese 조합이 없음!
→ 그럼 취미와 언어가 독립적이라고 보기 어렵다
→ Student ⟶⟶ Hobby or Student ⟶⟶ Language 중 적어도 하나는 성립하지 않음

---

💡 핵심 포인트 요약

개념 설명

다치 종속 X ⟶⟶ Y	같은 X에 대해, Y와 나머지 속성이 모든 조합이 되게끔 튜플이 존재해야 한다
모든 조합이란?	Y의 가능한 값들과, Z의 가능한 값들 간의 직접곱(조합)
MVD 성립 조건	그 조합들이 릴레이션에 모두 존재해야 성립한다

---

다치 종속 정리

"같은 X 값을 가진 튜플들 사이에서,
Y와 나머지 속성(Z)이 전혀 관련 없이,
자유롭게 모든 조합을 이룰 수 있다면 → X ⟶⟶ Y"

 
 

 

A와 B는 sets of attributes일 수 있다.
A bar, B bar: 축약해서 표현하는 것
 
위 판서 설명
B values와 rest values가 독립적이어서 모든 조합이 있는 형국
 
따라서 가끔 multi-value dependencies를 tuple generating dependencies라고 부른다.
정의가 기존의 튜플이 있을 때, 추가적인 튜플들을 가지는 것에 대한 것이기 때문.
 
ex. relation R(A,B,C)가 있고, multivalued dependency A  ↠ B일 때, 의미
for each value of A, we must have every combination of B and C values.
when you have A multi determines B,
then you also have A multi determines rest.

cName=college Name

* 대학에 선택적으로 취미를 공개한다 <=> 취미와 대학 간에 multivalued dependency가 없다.
* 학생, 대학, date가 주어졌을 때 전공이 다치 종속되고, 전공은 나머지와 독립적이다.
 
Q. For the relation Apply(SSN,cName,date,major) with functional dependency SSN,cName  date, what real-world constraint is captured by SSN  cName,date?
A. A student must apply to the same set of majors at all colleges.

Explanation

SSN ↠ cName,date says that (cName,date) and major are independent, i.e., all combinations of (cName,date) and major must be present for any college or major a student applies for.

 

The definition for a trivial multi valued dependency,
that either B is a subset of A,
or A union B are all attributes.
 
trivial MTD = 자명한 MTD
🎯 첫 번째 조건: Y⊆XY
🎯 두 번째 조건: X∪Y=RX ∪ Y = RX∪Y=R
 
* 첫 번째 조건(Y⊆XY)에 대하여
 
릴레이션 R(A, B, C)가 다음과 같을 때,

A	B	C
1	x	m
1	x	n

A,B ↠ A 가 왜 자명한지 이해해보자

A,B ↠ A의 의미

 
같은 A와 B값을 가진 튜플들을 모아서, 
그들의 A 값이 자유롭게 조합될 수 있어야 한다.
(X ↠ Y: 같은 X 값을 가진 튜플들끼리는, 그들의 Y값들이 독립적으로 모든 조합을 이뤄야 한다는 뜻이기 때문)
 
하지만 그 그룹은 이미 A, B가 똑같은 튜플들.
즉, A는 이미 같음. 조합이고 뭐고 필요 없음.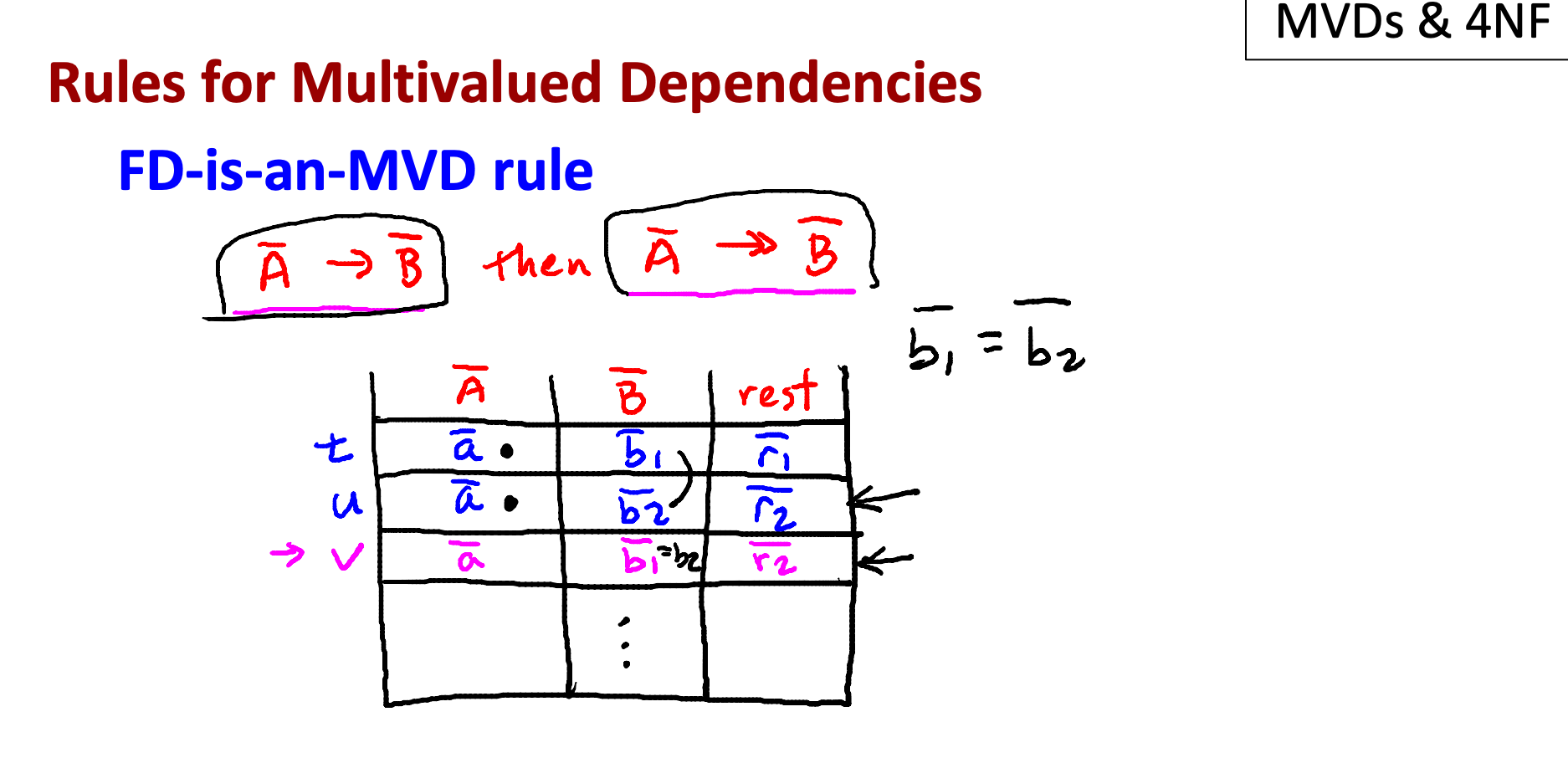

만약 A->B의 FD가 있다면,
A ↠ B 의 다치 종속도 이미 있다.
FD가 있다면 b1과 b2가 동일하다는 의미.
 
Every functional dependency is a multivalued dependency.

 
✅ intersection rule, transitive rule 찾아보기
Every functional dependency is a multivalued dependency.
따라서 모든 MVD에 관한 규칙은 FD에도 적용된다.
그 역은 성립하지 않는다. 벤다이어그램상!
 
예를 들어, splitting rule은 FD의 룰이지, MVD의 룰은 아니다.
 
✅ Splitting rule (=속성 분해 규칙)
함수적 종속을 여러 개로 나누어도 의미가 보존된다.
X -> YZ가 주어졌다면,
X -> Y, 그리고 X -> Z 로 나누어도 동일한 의미다.
 
같은 X값이면 Y와 Z도 같다.
이 말은
X가 같으면 Y도 같고, X가 같으면 Z도 같다는 의미를 내포하기 때문.
 
이 규칙은 FD 추론(closure 계산), 정규화 과정, 암스트롱 공리 등에서 쓰인다.
 
 

A가 키라면, b1=b2, r1=r2여야 한다.
4th normal form은 BCNF를 내포한다.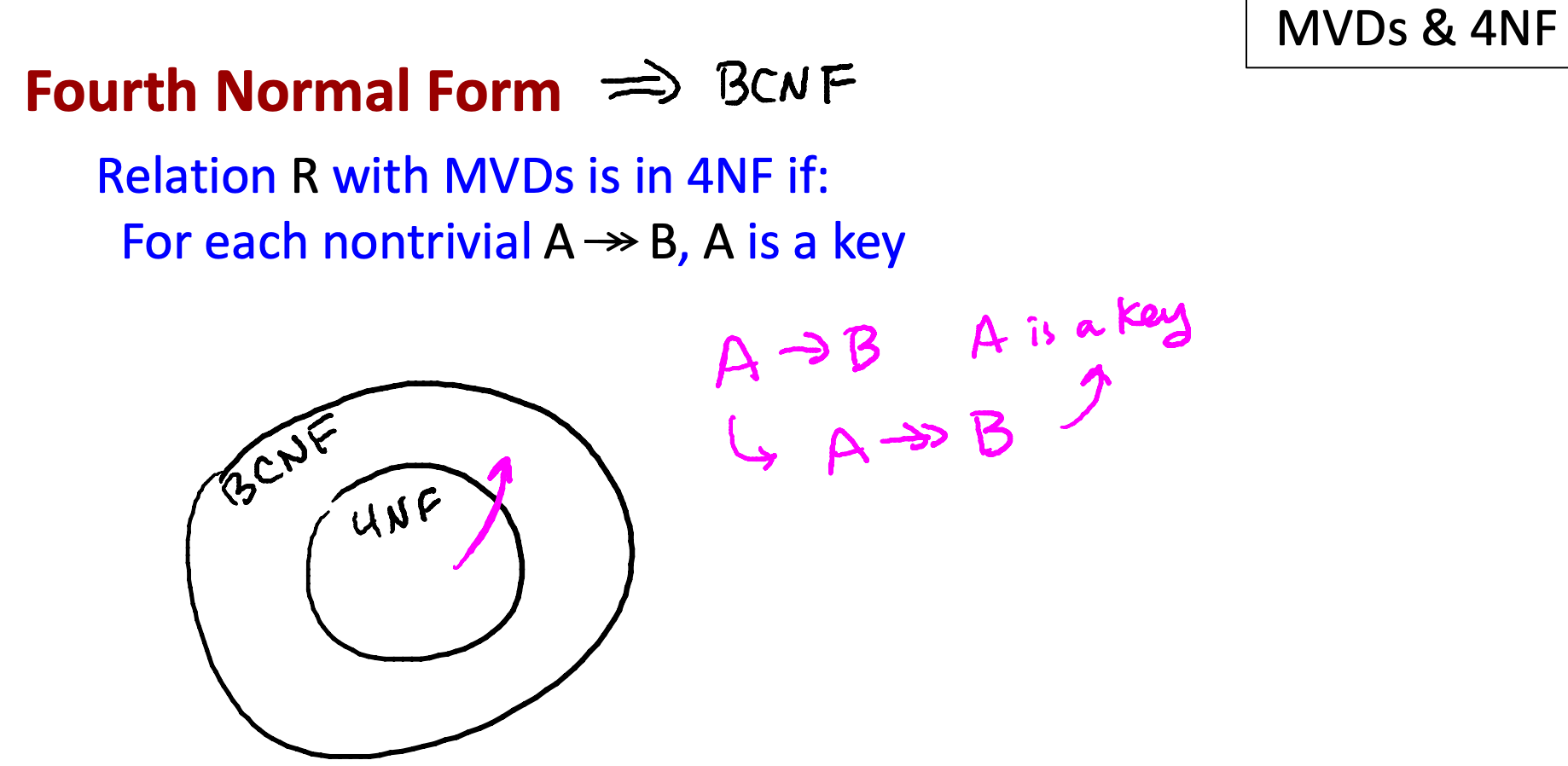

4NF가 BCNF를 내포하는 이유:
모든 함수적 종속(FD)은 다치 종속(MVD)의 특별한 경우이기 때문
 
FD는 MVD보다 더 약한 제약
 
 
FD ⊆ MVD 증명
 
릴레이션 R(X, Y, Z)에서
X → Y 에서 X ↠ Y 보이기.
 

• 같은 X 값을 가진 두 튜플 t₁, t₂ 가 있다고 하자
  • t₁ = (x, y₁, z₁)
  • t₂ = (x, y₂, z₂)
• 그런데 가정에 의해 X → Y 이므로
  • x가 같다면 y₁ = y₂ 이어야 함
  ⇒ 즉, 실제로 y₁ = y₂ = y 라고 하자 (항상 같은 값)
• 그럼 우리가 가질 수 있는 튜플들:
  • (x, y, z₁), (x, y, z₂) 가 이미 존재함
• 그러므로 가능한 모든 조합은 (x, y, z) 형태로 만들어짐
  → 즉, Y 값(y)은 항상 고정이므로,
  Y는 Z 값과 독립적으로 조합됨 (항상 y니까)
• 따라서 X ⟶⟶ Y 성립.

 

Q. Consider relation StudentInfo(sID, name, dorm, major) with functional dependency sID  name and multivalued dependency sID  dorm. What schema would be produced by the 4NF decomposition algorithm?
A.S1(sID,name), S2(sID,dorm), S3(sID,major)
Explanation

There is no key for the relation. Decomposing on the violating FD separates (sID,name) from (sID,dorm,major). Decomposing on the violating MVD separates (sID,dorm) from (sID,major). Now there are no violating FDs or nontrivial MVDs.

A ↠ B이면
A가 주어졌을 때 B 와 나머지는 모든 조합을 가진다.
B와 나머지가 독립적이라는 말.
따라서 (A,B)와 (A,나머지)를 따로 뺀다