(edX stanfordOnline Databases: Modeling and Theory) Functional Dependencies

https://www.edx.org/learn/databases/stanford-university-databases-modeling-and-theory

StanfordOnline: Databases: Modeling and Theory | edX

 

* Compression

함수적 종속(Function Dependencies)을 이용하면 데이터의 중복을 인식할 수 있다.

학번 -> 이름이라는 FD가 있다면, 같은 학번에 대해 이름이 반복 저장되는 것은 낭비다.

이런 FD를 기반으로 데이터를 압축(분리 저장 등)하면 저장 공간을 절약 할 수 있다.

 

* 모든 키는 함수적 종속이지만, 모든 함수적 종속이 키는 아니다.

FD는 더 일반적인 개념이다.

 

 

SSN: Social Security Number (학생들 각자에 고유하게 부여되는 번호)

HScode: High School Code

Functional dependency

A determines B for a relation R

 

속성이 각 side에 하나만 있을 필요는 없다.

set of attributes도 된다.

여러 속성이 있을 때는 bar로 표시한다.

 

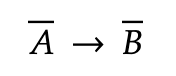
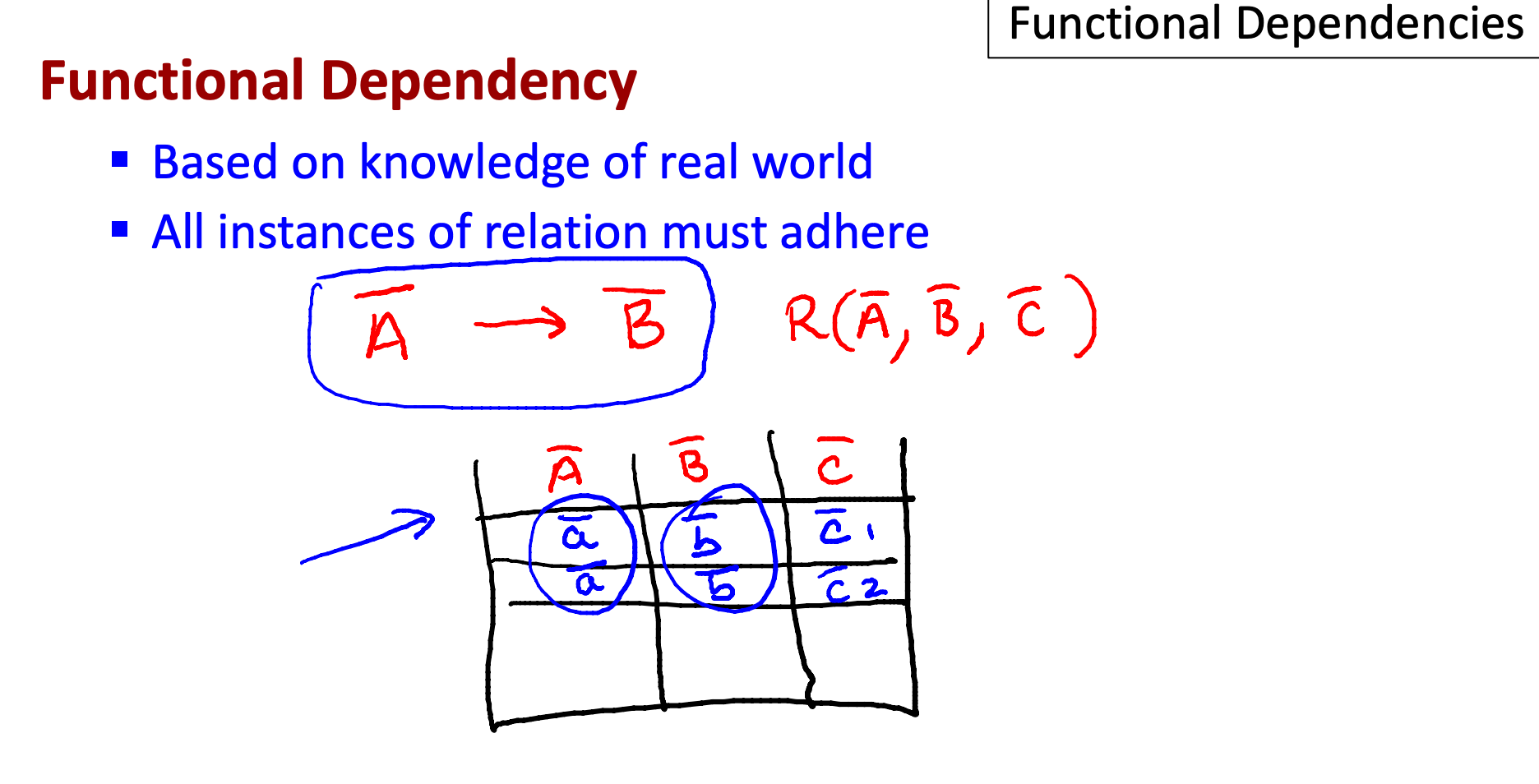
A bar: set of attributes A

set of attributes A functionally determines a set of attributes B

Any time tuples agree in their A values, they also agree in their B values.

 

앞서 나온 Student Relation, Apply Relation에서 FD를 정리해보자

SSN -> priority: transitive rule로 두 개 FD를 보고 이렇게 쓸 수 있다

cName이 unique할 때 FD

SSN = social security number, 학생을 결정한다.

CName(=college name)이 unique하다는 가정하에 이렇게 쓸 수 있다.

SSN, cName -> date: Every application from a student to a specific college must be on the same date.. (if a student applies to a college more than once, it must be on the same date.)

SSN -> state: 한 학생은 1주에 1개 대학교에만 지원할 수 있을 때

 

현실 세계의 제약 사항을 잘 파악하고 functional dependencies로 잘 translate 해야 한다.

그래야 좋은 relational design을 할 수 있다.

 

위의 경우 동일한 튜플이 2개가 된다.

그런데 동일한 튜플은 없다는 제약 사항이 있으므로...

동일한 set of attributes A(A bar)를 가질 수 없다.

set of attributes A는 키가 된다.

 

Functional Dependencies generalize the notion of keys.

Nontrivial FD 케이스: set of attributes B가 set of attributes A 에 포함되지 않는다.

=> 일부는 A에 포함되고, 나머지는 포함안 되는 케이스 생각하기

우측 사이드는 분할이 가능하다.

set of attributes A가 B1을 결정하고, B2를 결정하고...

그러나 좌측 사이드 분할은 불가능하다.
결합해야만 키가 되는데, 한 가지 속성만으로 우측 사이드를 결정할 수 없기 때문이다.

inverse(역) of the splitting rule

(1) Ā → B̄ 이면, Ā → Ā ∪ B̄

함수적 종속(FD)에서 Armstrong's Axioms 중 하나인 augmentation rule(확장 규칙)에 기반한 자명한 종속성(trivial dependency)의 성질을 다룬 규칙

A가 B를 함수적으로 결정한다면, A는 A와 B를 모두 결정한다.

 

(2) Ā → B̄ 이면, Ā → Ā ∩ B̄

B가 A의 부분집합이라면 Ā ∩ B̄는 B̄

 

 

closure is written using the + sign.

✅ Closure of Attributes란?

속성 집합 X의 closure, 표기: X⁺

→ 주어진 함수적 종속 집합 F로부터
X로부터 도출(추론)할 수 있는 모든 속성들의 집합

 

* 어떤 속성 집합 X가 후보 키인지 확인하려면 X⁺가 전체 속성 집합(R)과 같은지 보면 된다.

 

🔁 예시

관계 R(A, B, C, D)
함수적 종속 F = { A → B, B → C, A → D }

👉 A⁺를 구해보자

1. 초기: A⁺ = {A}
2. A → B 이므로 B 추가 → A⁺ = {A, B}
3. B → C 이므로 C 추가 → A⁺ = {A, B, C}
4. A → D 이므로 D 추가 → A⁺ = {A, B, C, D}
5. 종료: 더 이상 추가 없음

✅ 결과: A⁺ = {A, B, C, D}

→ 따라서 A는 후보 키가 될 수 있음 (모든 속성을 유도했으므로)

 

 

Q. Consider the relation R(A,B,C,D,E) and suppose we have the functional dependencies AB → C, AE → D, and D → B. Which of the following attribute pairs is a key for R?

1) AB

2) AC

3) AD

4) AE

 

 

Answer: 4. AE

Explanation: {AB}+ = {ABC}; {AC}+ = {AC}; {AD}+ = {ABCD}; {AE}+ = {ABCDE}

 

• S₁: 함수적 종속의 집합 (예: A → B, B → C)
• S₂: 어떤 함수적 종속 (예: A → C)

👉 이때 S₂가 S₁로부터 논리적으로 유도된다면,
즉 S₁ ⊨ S₂ (S₁ logically implies S₂) 라고 표현하며,
S₂ follows from S₁ 이라고도 말한다.

 

* Consider the relation R(A,B,C,D,E) and the set of functional dependencies S1 = {AB → C, AE → D, D → B}. 

S₂ follows from S₁인 S2들

S2 = {AD -> C}

S2 = {AD  -> C, AE ->  B}

S2 = {ADE -> BC}

 

Explanation

Using the FDs in S1: {AD}+ = {ABCD}; {AE}+ = {ABCDE}; {ABC}+ = {ABC}; {D}+ = {B}; {ADE}+ = {ABCDE}

 

* Does A -> B follow from S?

(1) closure로 체크

 

(2) Armstrong's Axioms: complete라고 불리는 룰

함수적 종속을 논리적으로 추론하기 위한 기본 규칙

세 가지 기본 규칙으로 모든 함수적 종속을 유도할 수 있다.

1. Reflexivity (반사성)

If Y ⊆ X, then X → Y

• 어떤 속성 집합 X가 있다면, 그 속성의 일부 Y도 X에 의해 결정된다.
• 직관: "내가 알고 있는 것(X)의 일부(Y)는 당연히 내가 알고 있음"

예:

• {A, B} → A
• {A, B, C} → {B, C}

---

2. Augmentation (증강성)

If X → Y, then XZ → YZ for any Z

• 종속관계에 같은 속성을 양쪽에 추가해도 여전히 유효하다.
• 직관: "A → B라면, A와 C를 함께 알면 B와 C도 알 수 있다"

예:

• A → B 이면, AC → BC
• AB → C 이면, ABD → CD

---

3. Transitivity (추이성)

If X → Y and Y → Z, then X → Z

• A가 B를 결정하고, B가 C를 결정하면, A가 C도 결정한다.

예:

• A → B, B → C 이면 A → C

 

용어	의미
Minimal set	불필요한 FD가 없는 최소한의 집합. 즉, 중복되거나 더 단순하게 표현될 수 있는 FD를 제거함.
Completely nontrivial	완전히 비자명한 FD. 오른쪽(RHS)이 왼쪽(LHS)에 포함되지 않음. (예: A → A는 자명(trivial), A → B는 비자명(nontrivial))
All FDs follow from	그 집합에 있는 FD들로부터 논리적으로 유도될 수 있는 모든 FD
hold on the relation	그 릴레이션에서 성립하다
such that A	A가 성립하도록

 

ex.

FD 집합:
F = { A → BC, B → C, A → B }

1. A → BC는 A → B, A → C로 나눌 수 있음 → 분해
2. A → C는 A → B와 B → C로 유도 가능 → 제거

→ 그래서 Minimal Cover는:
{ A → B, B → C }

 

FD는 relational design by decomosition을 하는 핵심 재료

Boyce-Codd 정규화를 하기 위해 Functional Dependencies를 이용한다.